Excelで対象行列に対するコレスキー分解(Cholesky decomposition)を算出するユーザー関数です。
Excelで振動の固有モードなどを算出する際に使用できます。
VBAコード
Option Explicit
Function Cholesky(X As Object)
'Cholesky decomposition
'original 6/14/2004,modified 11/22/2024
'Y.Urita
'declaration
Dim i As Integer, j As Integer, k As Integer, N As Integer
Dim a() As Double, U() As Double 'U() is upper right triangle matrix
Dim b1 As Double, b2 As Double, b4 As Double
N = X.Columns.Count 'Degree of freedom of matrix
ReDim a(1 To N, 1 To N), U(1 To N, 1 To N)
'initialize matrix A() & U()
For i = 1 To N
For j = 1 To N
a(i, j) = X.Cells(i, j).Value
U(i, j) = 0
Next j
Next i
'upper right triangle
'U11
b1 = Sqr(a(1, 1))
U(1, 1) = b1
'U1j
For j = 2 To N
U(1, j) = a(1, j) / b1
Next j
'Uii & Uij
For i = 2 To N
b1 = a(i, i)
b4 = 0
'Uii
For k = 1 To i - 1
b1 = b1 - U(k, i) ^ 2
Next k
b2 = Sqr(b1)
U(i, i) = b2
'Uij
If i < N Then
For j = i + 1 To N
b1 = a(i, j)
For k = 1 To i - 1
b1 = b1 - U(k, i) * U(k, j)
Next k
U(i, j) = b1 / b2
Next j
End If
Next i
'Output
Cholesky = U
End Function
説明
コレスキー分解はLU分解の一種ですが、正則な対称行列にのみ適用できます。
Aを対象行列、Lを左下三角行列、Uを右上三角行列としたときに
$$
A=LU=LL^t=U^tU
$$
という性質を持っています。
つまり、スカラーで言えば平方根を求める操作になります。
通常のLU分解とは違い、部分的ピボット選択は不要で計算コストも少なくて済みます。
右上三角行列Uを求める際は、対角項と非対角項に分けて計算を行います。
Aの要素をaij、Uの要素をuijとしたとき、
(1)対角項uii(j=i)の場合
$$
u_{ii}=\sqrt{a_{ii}-\displaystyle\sum_{k=1}^{i-1}u_{ki}^2}
$$
となります。
u11の場合は、総和を求める必要が無いため、
$$
u_{11}=\sqrt{a_{11}}
$$
となります。
(2)非対角項uijの場合
$$
u_{ij}=\frac{a_{ij}-\displaystyle\sum_{k=1}^{i-1}u_{ki}u_{kj}}{u_{ii}}
$$
となります。
1行目(i=1)であるu1jの場合も総和を求める必要がないため
$$
u_{1j} = \frac{a_{1j}}{u_{11}}
$$
となります。
使い方
例えば、下記のような対称行列のコレスキー分解を計算してみます。
$$
\begin{bmatrix}4&12&-16\\12&37&-43\\-16&43&98\end{bmatrix}
$$
3行3列の範囲を指定し、
=Cholesky(行列範囲)と入力し、CTRL+SHIFT+ENTERを押します。
CTRL+SHIFT+ENTERはExcelで配列数式を扱う際の操作になります。
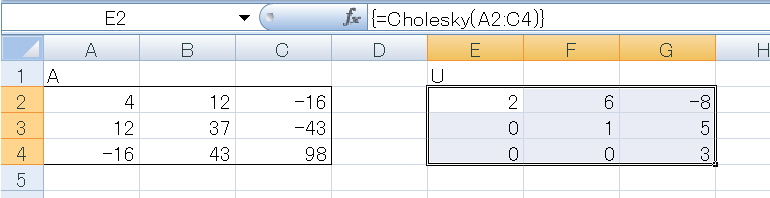
この例の行列の場合
右上三角行列Uは
$$
\begin{bmatrix}
2&6&-8\\
0&1&5\\
0&0&3
\end{bmatrix}
$$
となります。
参考資料
CQ出版社、VisualBasicによる固有値計算&振動解析プログラム、黒田英夫著
なお、現在は絶版となっていて、古本はプレミアの値段がついてしまっています。



コメント