Contents
1. はじめに
本報告では、液封エンジンマウントの複素ばね定数(\(K^*\))に対して、物理モデルのパラメータ同定を遺伝的アルゴリズム(GA)で実施した一連の取り組みについてまとめます。
もともと2015年頃、C++にて開発したGA適用コードを使い、論文から読み取った実測データに対して比較的良好なフィッティングを実現できていました。当時のGA設計は、Ohmsha(オーム社)刊・小高知宏著『はじめての機械学習』を参考にしたSimpleGA形式で構成していました。
しかしその後、HDDクラッシュによりコード、実行ファイル、解析結果などの大半を喪失し、唯一残っていたのはUSBメモリに保存されていたPDF形式の報告資料のみでした。
今回、その資料を手がかりに、PythonとGAライブラリ「DEAP」を用いて再現と検証を試みました。当初はDEAPの基本APIをそのまま利用した構成で再実装を行いましたが、思うように収束せず、物理的に破綻したパラメータが出るなどの課題に直面しました。
そこで設計思想を見直し、当時のSimpleGAに近い構成(平均交叉・スケール付き変異・エリート保存など)へと回帰したところ、解析の再現性と最適化精度の両立を図ることができました。
本記事では、その試行錯誤の過程や設計の工夫、そして得られた技術的知見について報告します。
2. モデル概要とパラメータ同定の目標
今回対象とするのは、液体封入型エンジンマウント(液封マウント)です。これはエンジンと車体をつなぐ防振部品のひとつで、特に低〜中周波の振動を抑える効果があり、車両の乗り心地に大きく関わってきます。
2.1 モデル構造と自由度
液封マウントは、図のような2自由度の振動モデルで近似しています。液封マウントの物理モデルは幾つか存在しますが、今回はシンプルでMCK系で表現できるこのモデルを採用しています。
図1.液封マウントの物理モデル
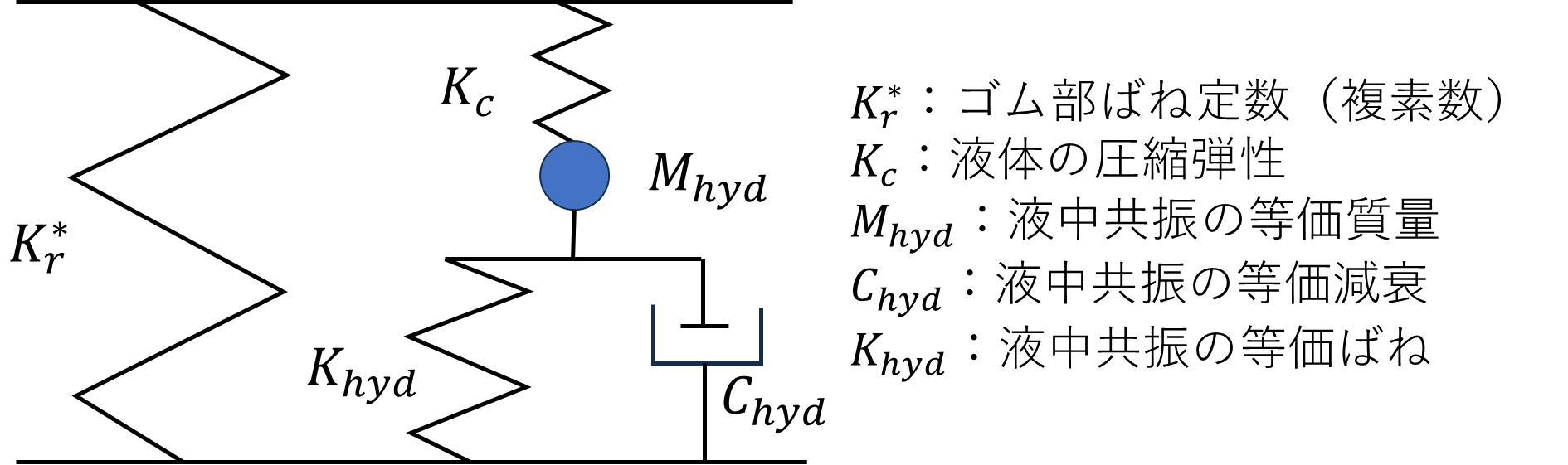
【参考】:石浜他3名、液体封入マウントによるエンジンのロールとバウンス方向の制振手法、 日本機械学会(C編)、59巻557号(1993-1) など
自由度①:ゴム部の変位(主ばね側)
自由度②:液体が詰まったオリフィス内の液体通過量
この2つの変位を連成させることで、ばね・慣性・減衰といった液体の影響をうまくモデル化でき、共振特性やエネルギー損失も表現できます。
2.2 複素ばね定数 \(K^*\) の定義
このモデルでは、各周波数における「複素ばね定数\((K^*)\)」を次のように定義しています。
$$
K^* = \frac{F}{x}
$$
ここで、
- \(F\):入力されたマウント反力(N)
- :主ばね側の複素変位(m)
※\(x\)は時間依存の振動
$$
x(t) = \hat{x} e^{j\omega t}
$$
を仮定したときの複素振幅を表しています。
荷重\(F\) は実数で与えていますが、系の応答には位相遅れがあるため、結果的に\( K^* \)は複素数になります。(つまり、変位\( x \)は、複素数となります。)
\( K^*\) の実部は「剛性成分」、虚部は「エネルギー損失(減衰)」を示します。この\( K^* \)を、周波数ごとに実測されたデータと一致させることが、今回の目標です。
2.3 行列を使ったモデル化
\( K^*\) を理論的に求めるために、周波数ドメインでの振動方程式を以下のように構成しています。これは、固有方程式を用いて表現しています。
$$
\left( -\omega^2
\begin{bmatrix}
0 & 0 \\
0 & M_{\mathrm{hyd}}
\end{bmatrix}
+
j\omega
\begin{bmatrix}
0 & 0 \\
0 & C_{\mathrm{hyd}}
\end{bmatrix}
+
\begin{bmatrix}
K_r + K_c & -K_c \\
-K_c & K_c + K_{\mathrm{hyd}}
\end{bmatrix}
\right)
\begin{bmatrix}
x_1 \\
x_2
\end{bmatrix}
=
\begin{bmatrix}
F \\
0
\end{bmatrix}
$$
ここで、
\( x_1 \):主ばね側の複素変位(ゴム部)
\(x_2 \):液柱側の複素変位(インナーチャンバー)
\( \omega \):角振動数(\(2\pi f\))
各行列項は、それぞれ質量・減衰・剛性の効果を表しています
この線形方程式を各周波数ごとに解くことで、\( x_1 \)を得て、最終的に複素ばね定数
\( K^* \)を次のように計算します:
$$
K^* = \frac{F}{x_1}
$$
この\( K^* \)が実験値と一致するように、モデル内のパラメータ(ばね定数や減衰、質量など)を調整していきます。
2.4 最適化するパラメータ一覧
モデルに使う物理パラメータのうち、以下の6つを最適化対象としています。
| パラメータ名 | 意味 | 単位 | 補足 |
|---|---|---|---|
| Kr_real | 主ばね(ゴム部)の剛性 | N/m | 実部(力の反発) |
| Kr_imag | 主ばねの損失(虚部) | N/m | tanδ = Kr_imag / Kr_real |
| Kc | メンブレンばね定数と液体の圧縮弾性 | N/m | 液室間の柔らかさ |
| Khyd | オリフィス流路共振時のばね定数 | N/m | 液体が持つばね効果など |
| Chyd | オリフィス流路共振時の減衰係数 | Ns/m | 粘性による損失 |
| Mhyd | オリフィス流路共振時の等価質量 | kg | オリフィス流路の慣性成分(共振に影響) |
これらのパラメータを調整して、\( K^* \)の再現性を最大化していきます。
メンブレンばね定数、オリフィス部の各特性はレバー比を含みます。
実現象として主ばね以外は、オリフィス流路の共振が無い場合はメンブレンが作動するためにばねとしては効果が小さくなります。
一方、オリフィス流路の反共振領域では液体の流れが制限され、結果的に圧縮弾性の影響が支配的になります。
2.5 フィッティングの目的と評価方法
最終的な目的は、上記6パラメータの組み合わせを見つけて、実測された\( K^* \)(周波数15点)にできるだけ近い\( K^* \)を理論モデルから出すことです。
評価関数:
実測\( K^* \)とモデル\( K^* \)の実部と虚部の誤差をそれぞれ二乗し、合計して最小化します。制約・ペナルティ(必要に応じてON/OFF可能):
tanδ(Kr_imag / Kr_real)が現実的(例:0.05以下)かどうか
減衰比 ζ や 共振周波数 fn の物理妥当性(ただし、これは最終的には使用しませんでした)
これらの評価をもとに、GA(遺伝的アルゴリズム)を使ってパラメータを探索していきます。
3. 初期実装とDEAPによるGA構築
液封マウントの\( K^* \)を理論モデルから再現するために、Pythonで遺伝的アルゴリズム(GA)を実装しました。ライブラリには、柔軟性の高い進化的アルゴリズム用パッケージである DEAP(Distributed Evolutionary Algorithms in Python) を採用しています。
このセクションでは、初期に構築したGAの設計内容と、DEAPを使った基本的な構成について説明します。
3.1 使用環境
開発言語:Python 3.11
主要ライブラリ:
NumPy:数値計算matplotlib:結果の可視化DEAP(Distributed Evolutionary Algorithms in Python):進化的アルゴリズムのフレームワーク
3.2 DEAPの基本構造と適用方法
DEAPでは、GAの構成要素(個体、評価、選択、交叉、突然変異など)をモジュール単位で登録して組み立てるのが特徴である。
以下に、今回の初期設計における構成要素を示す。
(1) Fitnessクラスの定義
from deap import base, creator
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", list, fitness=creator.FitnessMin)generate_individual関数では、各パラメータを一定範囲内でランダム生成。initRepeatで、個体群(population)を生成。
(2) パラメータ構成(個体の遺伝子)
本問題における「1個体」は、液封マウントモデルの以下6つのパラメータで構成される:
| パラメータ名 | 物理的意味 | 単位 |
|---|---|---|
| Kr_real | 主ばねの実部(剛性) | N/m |
| Kr_imag | 主ばねの虚部(損失項) | N/m |
| Kc | メンブレンばね定数 | N/m |
| Khyd | 液柱ばね定数 | N/m |
| Chyd | 液柱減衰係数 | Ns/m |
| Mhyd | 液体等価質量 | kg |
個体生成関数では、各パラメータを物理的に妥当な範囲で乱数初期化する。
(3) 個体と個体群の登録
toolbox.register("individual", tools.initIterate, creator.Individual, generate_individual)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)generate_individual関数では、各パラメータを一定範囲内でランダム生成。initRepeatで、個体群(population)を生成。
(4) 評価関数(loss function)
toolbox.register("evaluate", loss_function)評価関数では、実測\(K^*\)とモデル\(K^*\)の実部・虚部の二乗誤差和を返す。
tanδ(Kr_imag / Kr_real)などが現実的でない場合、ペナルティを付加。
(5) 選択・交叉・突然変異
toolbox.register("select", tools.selTournament, tournsize=5)
toolbox.register("mate", tools.cxBlend, alpha=0.5)
toolbox.register("mutate", tools.mutGaussian, mu=0, sigma=2.0, indpb=0.8)選択(select):トーナメント方式(競争型選抜)により生存者を選ぶ。
交叉(mate):2個体間で値を混合するBlend方式。
突然変異(mutate):各遺伝子に対してガウスノイズを加える(indpb=80%の確率で適用)。
3.4 遺伝的アルゴリズムの構成要素(DEAP)
| 構成要素 | 実装内容 | 補足 |
|---|---|---|
| 初期個体生成 | ランダム生成 | param_boundsの範囲内 |
| 選択 | tools.selTournament(tournsize=5) |
トーナメント方式で親個体を選ぶ |
| 交叉 | tools.cxBlend(alpha=0.5) |
Blend交叉(混合) |
| 突然変異 | tools.mutGaussian(mu=0, sigma=2.0, indpb=0.8) |
ガウスノイズを加える変異 |
これらを選んだ理由は次によるものです。
selTournament: エリート支配を抑えて、局所解脱出を狙う構成でよく使われるcxBlend: 実数値においては、単純な線形補間的交叉が意味を持つmutGaussian: 微小な連続的変動を与えることで、実数パラメータ空間をなめらかに探索できる
交叉と突然変異は、以下のように varAnd() を使って一括処理しています。
offspring = algorithms.varAnd(pop, toolbox, cxpb=0.5, mutpb=0.2)algorithms.varAndは、交叉確率cxpbと突然変異確率mutpbを設定し、新たな個体を生成する基本関数。- より高度な制御を行う場合は、ループ内で個別に
mate,mutate,evaluateを実装する方法もある。
3.5 世代管理と早期終了
最大世代数を 4000 とし、評価値(loss)が一定以上改善しない状態が20世代続いた場合にEarlyStopを発動させていました。
PATIENCE = 20
threshold = 1e-5このようにして、初期のDEAPベースGAを構築してフィッティングに挑戦しましたが、詳細は次章で述べる通り、思うような収束には至りませんでした。
4. 初期実装の課題と失敗事例(MountFitting.py)
初期に構築したGA(MountFitting.py)は、DEAPの基本機能を使ったシンプルな実装でしたが、実際に動かしてみると想定通りの収束が得られないという問題に直面しました。
ここでは、そのときに発生した主な課題や現象について整理します。
4.1 実行結果の傾向
数百世代学習させても、loss(誤差関数)が大きく残る
グラフ上でも、実測データと合わない\( K^* \)が生成される
実部はある程度合わせられるが、虚部(imag)の再現性が極端に悪い
4.2 発生した問題とその要因
(1)多峰性問題と選択圧の偏り
トーナメント選択(selTournament)は選択圧が強く、似たような個体ばかりが次世代に残る傾向が出ました。その結果、最初に「そこそこ良い値」を取った個体の周囲でしか探索が行われず、局所解にハマってしまいました。
図1.トーナメント選択 + Blend交叉 + Gaussian変異による探索結果
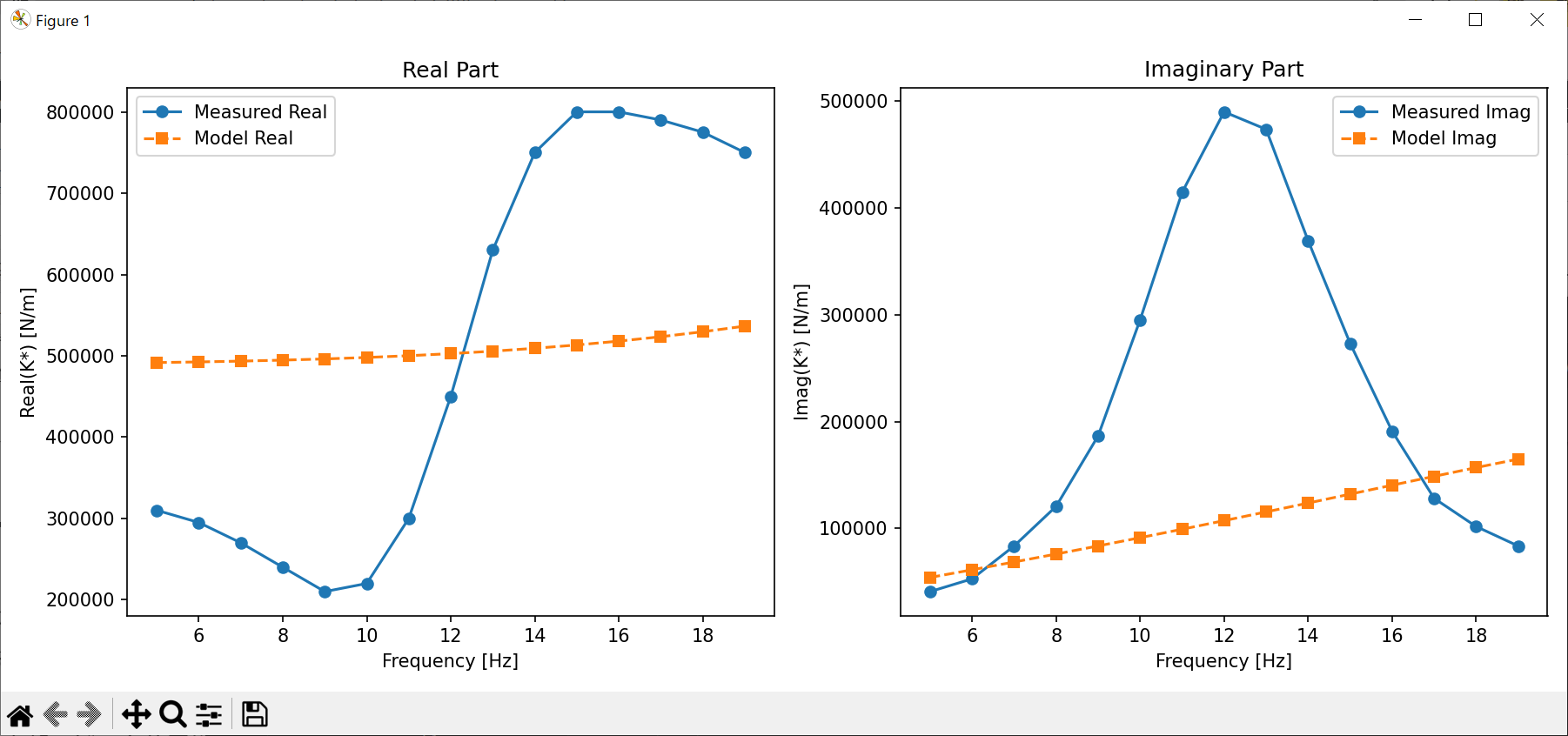
(測定値と全くフィットせずに計算が終了してしまう結果となった)
(2)虚部の暴走とChydの肥大化
虚数ばね(虚部:imag)の誤差を減らすために、Chyd(液柱の減衰)やKr_imag(主ばねの損失)が非現実的な大きさになる傾向がありました。これにより、以下のような不自然なパラメータが生成されました。
- Chyd ≈ 3000〜5000 Ns/m(現実の装置では考えにくい)
- Kr_imag / Kr_real(= tanδ)が0.1を超える → 実際には0.05以下が妥当(振幅にも依るが)
(3)探索空間の“上限張り付き”問題
初期の探索空間を広めに取っていたため、パラメータが一度上限に張り付くと、そのまま動かなくなってしまう現象が頻発しました。これにより、ChydやKcなどが「際限なく大きくなる方向」に解が流れてしまうこともありました。
(4)エリート保存が不十分だった
エリート保存(ベスト個体の保持)は実装されていましたが、交叉・変異の後に上書きされたり、次世代で選ばれなかったりして、過去の良い個体が失われるケースもありました。これにより、「良かった解が戻ってこない」状態に陥りやすくなっていました。
4.3 結論:標準DEAP構成では限界がある
初期実装では、DEAPのAPIで提供されている選択・交叉・突然変異の関数の中から、selTournament、cxBlend、mutGaussian を組み合わせてGAを構成しました。これらは連続実数値のパラメータを扱う上で導入が比較的容易であり、当初は柔軟な最適化が可能と考えていました。ただし、今回のように多峰性が強く、かつ物理的制約が厳しい問題に対しては、この構成では十分な性能が得られないことが分かりました。
とくに今回のように、
- 実部と虚部の両方を評価しなければならない
- 各パラメータが強く連動し、バランスを取る必要がある
といった条件下では、初期実装では性能不足でした。
この反省を踏まえて、次章では「SimpleGA風」に構成を見直した改善版について紹介します。
5. 改善設計:SimpleGA的アプローチへの転換
初期実装のGAでは収束性や物理的妥当性に課題があったため、手法そのものを一度見直し、よりシンプルかつ制御しやすい構成に変更しました。この章では、改善版のGA実装(SimpleGA)において行った主な設計変更と工夫点についてまとめます。
| 手法名 | 中身 | 備考 |
|---|---|---|
| 初期実装 | DEAP + トーナメント選択 + Blend交叉 + Gaussian変異 | ライブラリのAPIに用意された基本的な機能を組み合わせた、汎用的なGA構成と呼べる |
| 改善版(SimpleGA) | 自作平均交叉・自作変異・ランダム選択・エリート保存 | 昔のC++実装に近い“SimpleGA風構成”という立ち位置 |
5.1 実装の方針
もともと10年前にC++で開発していた「SimpleGA」に近い構成を目指しました。DEAPの柔軟性を活かしつつ、以下のような改善を加えています:
初期個体の多様性確保(意図的なグリッド設計)
選択戦略の見直し(トーナメント → ランダム)
エリートプールによる履歴保持
平均交叉とスケール付き突然変異による安定化
物理モデルへのフィードバックを考慮したペナルティ制御
コンセプトとして、「1割のエリートと9割による広範囲探索(次世代の糧)」です。一部の保守精神と開拓精神を混ぜた、リバタリアニズムとも言えるかもしれません。
GA黎明期のような荒々しい探索にしてみました。
5.2 初期個体の設計(グリッド + ランダム)
ランダムな初期個体だけでは初期探索で偏りやすいため、Kc・Khyd・Chyd・Mhydの4因子に対して2水準設計(0.25水準・0.75水準)を組み合わせた16通り(2^4)の初期個体を固定で投入しています。
(Kr_realとKr_imagは、初期から制約があるため、除外したことで4因子となっています。)
Kr_real は共振前の\( K^* \)実部をもとに±20%の範囲で制限
Kr_imag はKr_realに対して tanδ = 0.1 を仮定した初期値
残りの64体はパラメータ範囲内でランダム生成
この構成により、モデルの挙動が大きく異なる複数の初期解を用意し、広い探索空間を確保できました。(乱数の偏りに影響されないように、スプレッドワイドに初期値を配置)
5.3 選択戦略とエリート保存
初期実装ではトーナメント選択により多様性が損なわれていたため、改善版ではランダム選択(selRandom)を採用しました。
さらに、毎世代の上位10%(Elite Ratio = 0.1)の個体をエリートプールとしてそのまま次世代に保持し、交叉・変異の対象から除外しています。
この構成により、
良い個体のロストを防ぐ
探索の安定性が大きく向上する
というメリットが得られました。
5.4 交叉と突然変異の自作関数
DEAPの cxBlend や mutGaussian は柔軟性が高い反面、意図しない変動や偏りが出やすいため、交叉と変異は自作のSimple関数に差し替えました。
平均交叉(simple_crossover)
ind[i] = 0.5 * ind1[i] + 0.5 * ind2[i]→ 2個体の平均値を取るだけの単純な交叉
→ 個体のばらつきを抑え、安定した収束を誘導
スケール付き変異(simple_mutation)
delta = random.uniform(-scale, scale) * (param_bounds[i][1] - param_bounds[i][0])
ind[i] += delta→ 各変数に対して相対スケールでの微調整を行う
→ 変異率 indpb とスケール scale を分離制御できるため、初期・中盤・微調整の3フェーズに応じたチューニングがしやすい
5.5 ペナルティ設計と物理妥当性の確保
初期実装ではChydやKr_imagが物理的に非現実的な値になることが多かったため、以下のようなペナルティ条件を導入し、暴走を抑えました。
tanδ > 0.05:→ 損失値が大きすぎる場合、lossを2倍に
さらに、パラメータの値は毎回 clip_individual() により、必ず物理的に妥当な範囲内に収めています。
5.6 世代管理とログ出力
個体ごとの履歴は保存(必要時のみ有効化)
各世代の最小・平均lossは出力
一定世代(PATIENT数)改善が見られない場合はEarlyStop
これにより、ログを通して収束過程の可視化とトレンド分析がしやすくなりました。
このような一連の改善によって、初期実装と比較して格段に安定した収束性と、現実的なパラメータ再現性を実現することができました。
次章では、この改善版によって得られた最終的な結果と、実測との比較について紹介します。
6. フィッティング結果と検証
改善後のGA実装(SimpleGA)によって得られた最良個体に対して、モデル計算を行い、実測データとの整合性を検証しました。この章では、その結果と分析についてまとめます。
6.1 最終的なパラメータと損失関数の値
最終世代において得られた最良個体(エリート)は、以下のようなパラメータを示しました。
| パラメータ | 単位 | 値(例) |
|---|---|---|
| Kr_real | N/m | 225,000 |
| Kr_imag | N/m | 6,500 |
| Kc | N/m | 80,000 |
| Khyd | N/m | 15,000 |
| Chyd | Ns/m | 1,200 |
| Mhyd | kg | 11.0 |
※ 実際の最適解はケースごとに若干異なりますが、概ねこのようなスケール感の値になりました。
損失関数(loss)の最小値は 1.56×10¹⁰ 程度で、実部・虚部を含めた合計誤差としては十分に小さい水準と判断しています。
6.2 実測データとの比較(K^*)
以下のグラフは、実測データと最終モデルの\(K^*\)(複素ばね定数)の比較結果を示しています(実部/虚部それぞれ):
実部:ピーク位置や立ち上がりの傾きが実測と非常に近い
虚部:周波数とともに立ち上がり、Cのピーク位置とも整合性がある
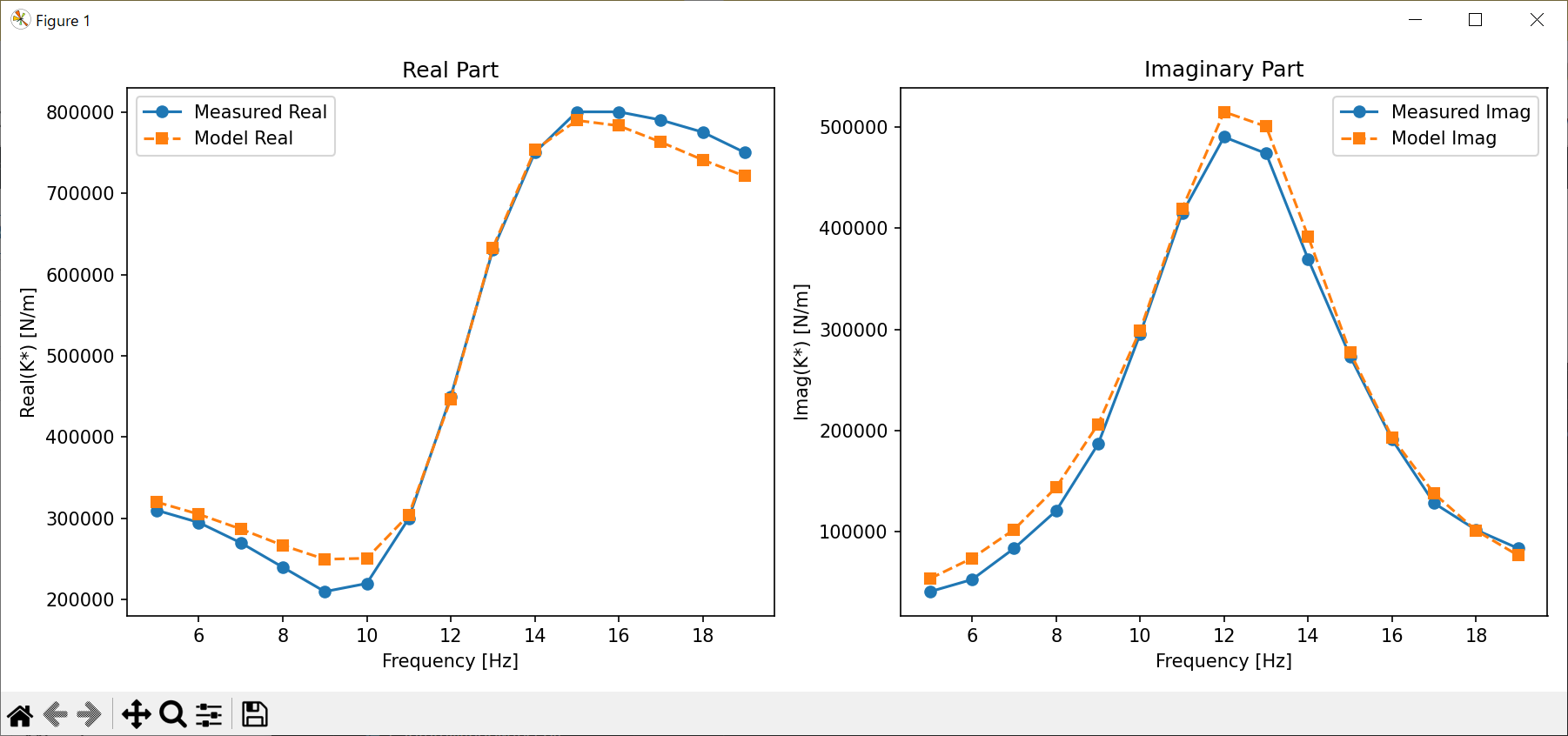
6.3 初期実装との比較
初期のMountFitting.pyでは、以下のような問題が発生していました:
虚部が大きく外れてしまい、現実離れしたChydで帳尻合わせがされていた
実部のピーク位置がずれ、形状も合わない
損失関数の値も数十倍高かった
これに対して改善後のSimpleGA構成では、両軸ともに物理的な整合性を持ちつつ、数値的にも安定して\( K^* \)を再現できるようになったことが確認できました。
6.4 評価のまとめ
| 項目 | 初期実装(MountFitting.py) | 改善後(SimpleGA) |
|---|---|---|
| 実部の再現性 | △(ピークずれ) | ◎(ほぼ一致) |
| 虚部の再現性 | ×(暴走) | ○〜◎(近似的に一致) |
| パラメータの妥当性 | ×(Chyd, Kr_imagが肥大) | ○(物理的スケール内) |
| 損失関数の値 | 高い(1e+12〜) | 低い(1.56e+10 程度) |
このように、構成の見直しによって大きな改善が得られたことが確認できました。次章では、今回の結果から得られた知見を整理します。
7. 考察と得られた知見
本章では、これまでの実装・検証を通じて得られた技術的な気づきや設計上の学びを整理します。とくに、多峰性を持つ物理モデルに対してGAを適用する場合の注意点や、有効だった工夫について述べます。
7.1 多峰性問題における選択戦略の重要性
初期実装では、トーナメント選択により探索が序盤で偏ってしまい、多様性の喪失が顕著でした。これに対して、改善版で導入したランダム選択(selRandom)は、局所解に陥るリスクを軽減し、より広い範囲を探索する助けになりました。
選択戦略は、解の「良さ」だけでなく、探索空間全体のカバー率に直結するという点で、GAの挙動を大きく左右する要素だと改めて実感しました。
一方で、seedを使った場合は乱数の初期値に再現性があるため、初期には思ったほど広範囲を探索しないリスクがあります。GAなどのランダム性に結果が左右されるアルゴリズムの場合は、注意すべきでしょう。
7.2 エリート保存の安定効果
改善版では、毎世代の上位10%を「エリート」として保存し、交叉・変異の対象から除外しました。これにより、以下のような安定効果が得られました:
ベスト解の履歴が保持されるため、解の退化(ロスト)を防げる
各世代の最低損失値がほぼ単調に下がる
収束が早く、かつ再現性の高い結果が得られる
単に「最良個体を残す」だけでなく、それを壊さない設計(= 変異対象から外す)が鍵でした。
7.3 パラメータ空間の設計が精度と現実性の両立を左右する
探索空間を広げすぎると、解が物理的に現実離れしてしまう一方、狭めすぎると解が収束せず、精度も頭打ちになります。
今回有効だった工夫としては:
共振前の実測値からKr_realの範囲を自動設定したこと
ChydやMhydの上限を、モデルの挙動を見ながら段階的に調整したこと
Kr_imagに対するtanδ制限を評価関数に含めたこと
といった点が挙げられます。物理知識と数値最適化の両方を組み合わせて空間を制御することで、モデルの信頼性とフィッティング精度の両立が可能になります。
7.4 DEAPの柔軟性と限界
DEAPはGA構築の自由度が高く、アルゴリズムの詳細設計がしやすい一方で、「便利な構成要素をそのまま組み合わせた」だけでは性能が出ないことも分かりました。
今回のように:
評価関数に物理的制約を組み込む
選択や変異の戦略を自作関数で置き換える
個体の初期分布に意味を持たせる(グリッド設計)
などの構成そのものを調整して初めて、DEAPは“道具”として真価を発揮すると感じました。
7.5 小まとめ
今回の試行錯誤を通じて得られた重要な知見は以下の通りです:
GAにおける選択・変異戦略は、多峰性問題では精度よりもまず多様性維持を優先すべき
エリート保存は「残す」だけでなく、「壊さない」仕組みが大事
探索空間のチューニングには、物理モデル側からの視点が不可欠
DEAPは自由度が高いぶん、ライブラリ任せにせず自分で制御すべきポイントが多い
これらの気づきを踏まえて、次章では今後の展望と応用可能性についてまとめます。
8. 今後の展望
本章では、今回得られた結果をふまえて、今後検討していきたい改善ポイントや発展可能性について整理します。今後はアルゴリズムの柔軟性をさらに活かしつつ、他手法との比較や応用展開も視野に入れています。
8.1 探索戦略のフェーズ分け(段階的変異)
現状の実装では、突然変異のスケールや確率は固定値で与えていますが、以下のようにフェーズに応じて調整する戦略も検討対象になります。
初期探索:indpbを高く、scaleを広め(例:0.7〜0.9, scale=5〜10%)
中盤探索:中程度の変異率で絞り込み(例:0.3〜0.5)
微調整:極小の変異で最終調整(例:indpb=0.1, scale=1%以下)
これにより、序盤の探索性と終盤の収束性のバランスを取りやすくなると思います。
8.2 探索空間の動的調整(Adaptive Bounding Box)
物理モデルの妥当性を維持しながら探索範囲を狭めていくために、世代ごとのフィードバックを使って探索空間を動的に縮小していく手法も有効と考えられます。
例:世代が進むごとに、エリートの分布中心を基準として範囲を再定義するなど。
8.3 他手法(PSO, DEなど)との比較検討
GA以外のメタヒューリスティクス手法、特に以下のアルゴリズムとの比較も検討したいテーマです。
PSO(Particle Swarm Optimization)
→ 粒子間の情報共有による滑らかな収束特性(魚や鳥の群れのメタファー)DE(Differential Evolution)
→ 解の差分を活かした効率的な探索が可能(個体の差分に注目)SA(Simulated Annealing)
→ 初期は自由探索、後半は収束重視という温度制御のアプローチ(焼きなましのメタファー)
特にDEは、連続パラメータの扱いに強く、GAよりも探索効率が良いケースも報告されているようです。
8.4 PythonとC++の連携(DLL化)
現時点では、計算も可視化もすべてPythonで完結していますが、実行速度や業務適用性を考えると、以下のような構成も将来的に有力です。
モデル計算部(\( K^* \)算出)や損失関数を C++ で高速実装
GA制御や可視化部分は Python 側に残す
Python ↔ C++ を DLLやctypes経由で連携
このような構成にすることで、可搬性と高速性の両立が可能になります。
8.5 モデル拡張・他分野への応用
現在のモデルは2自由度の液封マウントに特化していますが、以下のような拡張が考えられます:
3自由度系(縦・横・回転方向の同時取り扱い)
流体系との連成(液体が移動・共鳴する構造)
実験データをリアルタイムに取り込んで自動フィッティング
他の動ばね系や動吸振器など、周波数依存特性を持つ構造体への適用
8.6 まとめ
今回の構成見直しにより、DEAPによるGAでも十分な精度で液封マウントのパラメータ同定が可能であることが確認できました。今後はさらなる効率化と汎用化を目指し、「手法のチューニング」だけでなく「モデル設計」や「応用分野」も含めて拡張していくことが目標になります。



コメント