FFT前処理で迷わない！窓関数の違いを比較【用途別の選び方も解説】

はじめに

FFTを使って信号の周波数成分を分析する際、
「本当にそのままFFTにかけていいのか？」という問題があります。

実は、信号をそのままFFTすると“リーク（leakage）”という現象が発生し、
本来ないはずの周波数成分が現れてしまうことがあります。

そのリークを抑えるために使われるのが「窓関数（Window Function）」です。

---

窓関数とは？

• 信号の前処理として使われる「重み付け」
• FFTの結果に大きく影響を与える
• 主にローブ幅とサイドローブ（漏れ）の高さが変わる

メインローブとサイドローブ

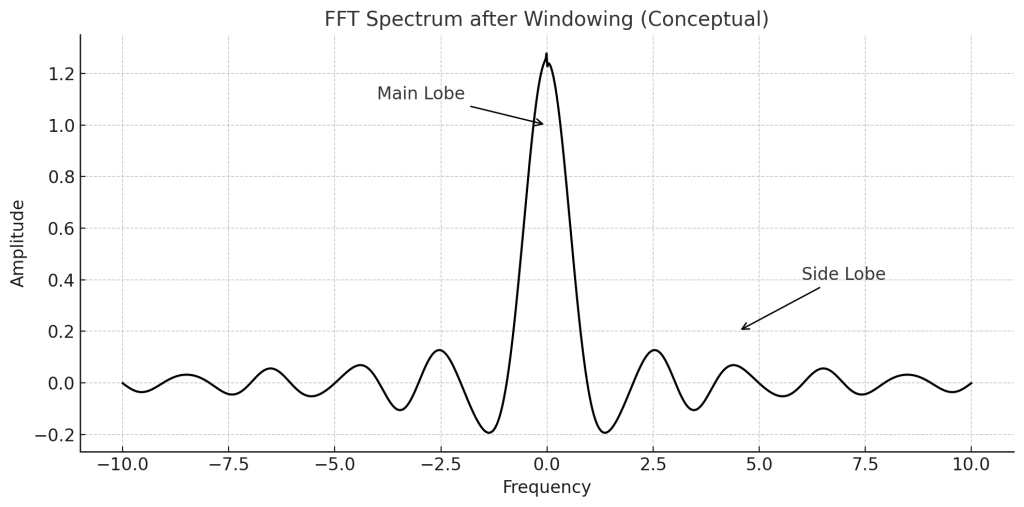
FFTの振幅スペクトルは、実数信号であればナイキスト周波数を境に左右対称になります。
通常は 0Hz〜ナイキスト周波数の範囲のみを解析対象とします。

※この図では、わかりやすさのために「0Hz付近にピークがある信号（低周波成分が強い信号）」を例にしています。

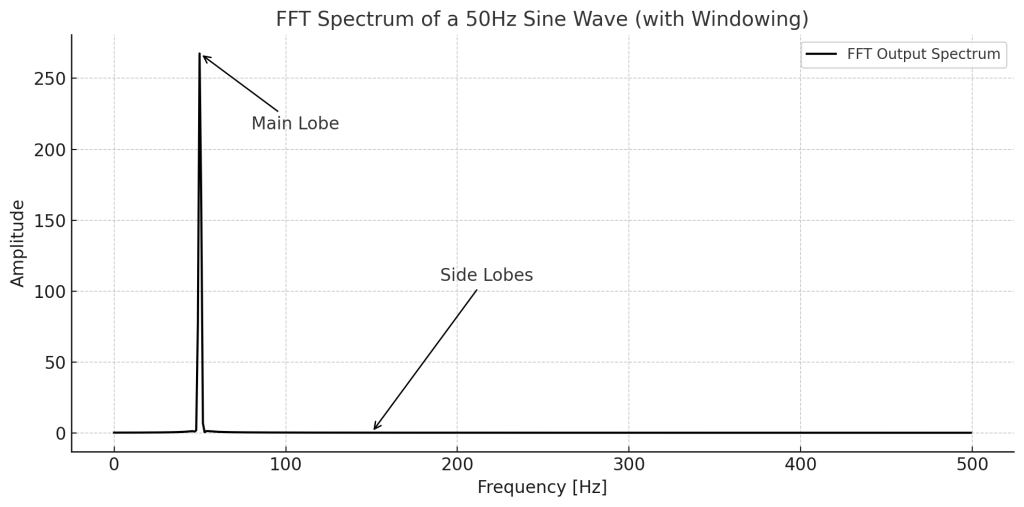
本来、純粋な50Hzのサイン波のスペクトルは「50Hzに1本のピーク（｜）」が立つだけです。（図3）
しかし、有限区間で信号を切り出すと、解析上は“理想のピーク”が広がりを持つ「山」になり、
その周囲にも小さな山（サイドローブ）が現れます。

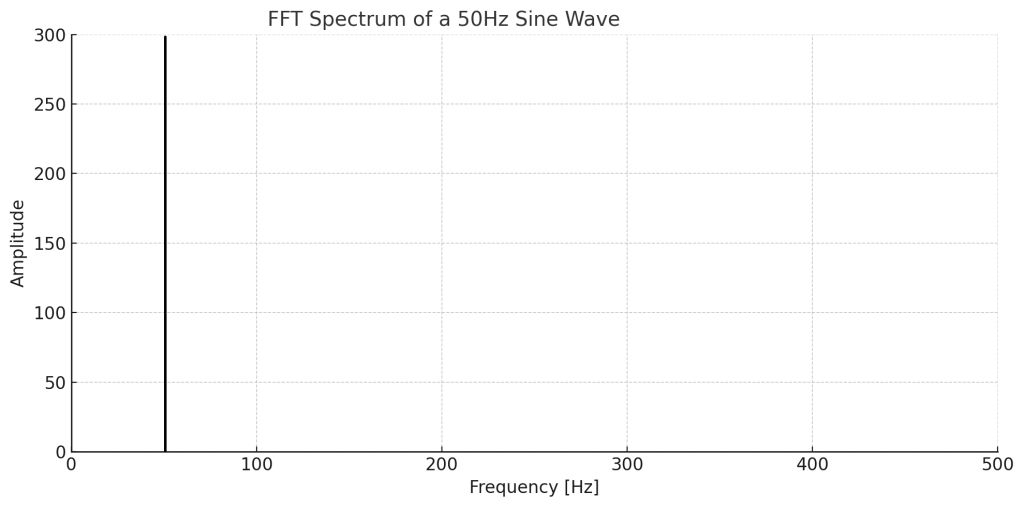
※この「ピーク1本だけ」の形は、理論上の理想スペクトルです。実際には存在しない信号（∞長の連続サイン波）です。

🔸 ローブ幅（メインローブ幅）とは？

FFTで出力されるスペクトルには、ピークの周囲に「山型の広がり」ができます。
この中央の大きな山部分が「メインローブ」です。

• このメインローブの「横幅」が広いと、近くの周波数成分を区別しにくくなる（分解能が下がる）
• 狭いとシャープに見えるが、代わりにサイドローブ（漏れ）が強くなる傾向があります

🎓 メモ：分解能を重視したい時は「メインローブが狭い窓」を選びます

---

🔸 サイドローブとは？

メインローブの横に小さなギザギザの山（波打ち）が出ることがあります。
これが「サイドローブ（副次ローブ）」です。

• これは元の信号に含まれない「偽の周波数成分（リーク）」として現れます
• サイドローブが高いと、本来無い成分が見えてしまい、誤った判断を招くことも

🎯 リークを抑えたいなら、サイドローブが小さい窓関数（例：Blackman, Flat-top）を選ぶのがセオリーです

窓関数一覧と良く使われる窓関数たち

各ウインドウのメリット・デメリット比較表

ウインドウ関数	メリット	デメリット	向いている波形
矩形（Rectangular）	周波数分解能が最高、エネルギー損失なし	サイドローブが高く、スペクトルリークが大きい	突発的な信号（パルス）、狭帯域信号
ハン（Hann） / ハニング（Hanning）	サイドローブを抑え、分解能とリークのバランスが良い	矩形より周波数分解能が低い	周期的な信号、一般的なスペクトル解析
ハミング（Hamming）	サイドローブをさらに抑え、振幅誤差が少ない	メインローブが広くなり、周波数分解能が低下	音声信号、通信信号
ブラックマン（Blackman）	サイドローブを大幅に抑えられる	メインローブが広がり、分解能が低い	ノイズの多い信号、スペクトルリークを抑えたい場合
ブラックマン・ハリス（Blackman-Harris）	サイドローブが非常に低い（-92 dB）	メインローブが最も広く、周波数分解能が悪化	雑音の多い環境、広帯域信号
フラットトップ（Flat-top）	振幅精度が高く、正確なパワースペクトル測定向け	メインローブが極めて広く、分解能が大きく低下	パワースペクトル測定（FFTスペクトラムアナライザ）
カイザー（Kaiser）	β パラメータでサイドローブと分解能を調整可能	設定が必要で、計算負荷が高い	特定の用途向け、カスタム設計が必要な場合

よく使われる窓関数たち（ざっくり特徴比較）

窓関数	メインローブ幅	サイドローブ減衰	特徴
Rectangular（矩形）	狭い	弱い	周波数分解能は高いがリークが強い
Hamming	中	強い	バランス型、一般的によく使われる
Hann	やや狭い	中	Hammingに似るが減衰はやや弱め
Blackman	広い	非常に強い	リークを最小化したい時に最適
Flat-top	広い	超強い	正確な振幅測定に強い（スペアナなど）

どの窓を使えばいいの？用途別ガイド

使用目的	推奨窓関数	理由
一般的なFFT解析	Hamming	バランスが良く、広く使われている
振幅をできるだけ正確に知りたい	Flat-top	振幅誤差を最小化する設計
とにかくリークを抑えたい	Blackman	サイドローブの減衰が非常に強く、ノイズに強い
周波数のピークを分離したい	Rectangular	分解能が高くピークの位置を見極めやすい

---

おわりに

窓関数は「FFTの前につけるおまけ」ではなく、
信号解析の精度を大きく左右する重要な処理です。

この記事が、あなたの用途に合った窓関数選びの参考になれば幸いです。

おまけ

Pythonでlibrosaライブラリを使ったときの窓関数の指定

1. boxcar: 矩形窓
2. triang: 三角窓
3. blackman: ブラックマン窓
4. hamming: ハミング窓
5. hann: ハン窓
6. bartlett: バートレット窓
7. flattop: フラットトップ窓
8. parzen: パーゼン窓
9. bohman: ボーマン窓
10. blackmanharris: ブラックマン・ハリス窓
11. nuttall: ナットール窓
12. barthann: バートレット・ハン窓
13. kaiser: カイザー窓（βパラメータが必要）
14. gaussian: ガウス窓（標準偏差が必要）
15. general_gaussian: 一般化ガウス窓（標準偏差と形状パラメータが必要）
16. dpss: ディスクリート・プロレト・スペクトル・シーケンス窓（トレードオフパラメータが必要）
17. chebwin: チェビシェフ窓（サイドローブ抑制が必要）