Excelユーザー関数:実固有値・固有ベクトル算出

Excelで対象行列に対する固有値と固有ベクトルを算出するユーザー関数です。

Excelで主成分分析、慣性テンソルから主慣性モーメントなどを算出する際に使用できます。

Contents

1 VBAコード
2 説明
3 使い方
4 参考資料

VBAコード

VBA
Option Explicit

Function Eig(X As Object)
'Real Eigen Value by Jacobi method
'This function for Real symmetric matrix only
'original 6/14/2004 , modified 12/28/2004 ,modified 11/13/2024
'Y.Urita

    'declaration
    Dim i As Integer, j As Integer, N As Integer
    Dim K_new As Integer
    Dim i_rot As Integer, j_rot As Integer, K_max As Integer
    Dim a() As Double, v() As Double
    Dim b1 As Double, b2 As Double, b3 As Double
    Dim Eps As Double, K_iter As Double
    Dim ax As Double, v_cos As Double, v_sin As Double, v_tan As Double
    Dim ev() As Double
    
    'matrix size
    N = X.Columns.Count
    
    ReDim a(1 To N, 1 To N), v(1 To N, 1 To N), a2(1 To N), ev(1 To N, 1 To N + 1)
    
    'define acceptable error rate
        Eps = 10 ^ -16
    'max itaretion number
        K_max = 4000
        
    'initialize matrix A()
        For i = 1 To N
            For j = 1 To N
                a(i, j) = X.Cells(i, j).Value
            Next j
        Next i
        
    'initialize matrix V()
    'V : unit matrix
        For i = 1 To N
            For j = 1 To N
                v(i, j) = 0
            Next j
        Next i
        
        For i = 1 To N
            v(i, i) = 1
        Next i
        
        
    'iteration for that all nondiagonal elements are 0
    
    Do
        K_iter = K_iter + 1 'add itaration number
        K_new = 0 'flag :if nondaigonal elemnt has unacceptable error, flag was 1
    
            ax = 0
            
            'looking for maximum element and replace ax
            For i = 1 To N
                For j = i + 1 To N
                    b1 = Abs(a(i, j))
                    If b1 > ax Then
                        i_rot = i
                        j_rot = j
                        ax = b1
                    End If
                Next j
            Next i
            
            If ax > Eps Then
            K_new = 1
            
            'calculate cosine and sine
            b1 = a(i_rot, i_rot) - a(j_rot, j_rot)
            b2 = -b1 - Sqr(b1 ^ 2 + 4 * ax ^ 2)
            b3 = 2 * a(i_rot, j_rot)
            v_tan = b2 / b3
            v_cos = 1 / Sqr(1 + v_tan ^ 2)
            v_sin = v_cos * v_tan
            
            'rotate V vector
            For i = 1 To N
                b1 = v(i, i_rot)
                v(i, i_rot) = v_cos * b1 + v_sin * v(i, j_rot)
                v(i, j_rot) = v_cos * v(i, j_rot) - v_sin * b1
            Next i
            
            'rotate A matrix
            For i = 1 To i_rot - 1
                b1 = a(i, i_rot)
                a(i, i_rot) = v_cos * b1 + v_sin * a(i, j_rot)
                a(i, j_rot) = v_cos * a(i, j_rot) - v_sin * b1
            Next i
            
            For i = i_rot + 1 To j_rot - 1
                b1 = a(i_rot, i)
                a(i_rot, i) = v_cos * b1 + v_sin * a(i, j_rot)
                a(i, j_rot) = v_cos * a(i, j_rot) - v_sin * b1
            Next i
            
            For i = j_rot + 1 To N
                b1 = a(i_rot, i)
                a(i_rot, i) = v_cos * b1 + v_sin * a(j_rot, i)
                a(j_rot, i) = v_cos * a(j_rot, i) - v_sin * b1
            Next i
            
            'erase nondiagonal element
            b1 = a(i_rot, i_rot)
            b2 = 2 * v_cos * v_sin * a(i_rot, j_rot)
            b3 = v_cos ^ 2 * b1 + b2
            
            a(i_rot, i_rot) = b3 + v_sin ^ 2 * a(j_rot, j_rot)
            b3 = v_cos ^ 2 * a(j_rot, j_rot) + v_sin ^ 2 * b1
            a(j_rot, j_rot) = b3 - b2
            a(i_rot, j_rot) = 0
            a(j_rot, i_rot) = a(i_rot, j_rot)
        End If
    Loop While K_iter < K_max And K_new > 0
    
    'output
    For i = 1 To N
        ev(i, 1) = a(i, i)
        For j = 1 To N
            ev(i, j + 1) = v(i, j)
        Next j
    Next i
    
    'eigenvalue & eigenvector
    Eig = ev

End Function

説明

ヤコビ法を使って、対称行列に対し回転行列で相似変換をします。

$\begin{bmatrix}cos\theta&sin\theta\\-sin\theta&cos\theta\end{bmatrix} \begin{bmatrix}a_{11}&a_{12}\\a_{12}&a_{22}\end{bmatrix} \begin{bmatrix}cos\theta&-sin\theta\\sin\theta&cos\theta\end{bmatrix} = \begin{bmatrix}a_1&0\\0&a_2\end{bmatrix}$

左辺を展開すると

$\begin{bmatrix}a_{11}cos^2\theta +2a_{12}sin\theta\cos\theta +a_{22}sin^2\theta& a_{12}(cos^2\theta-sin^2\theta)+(a_{22}-a_{11}sin\theta\cos\theta\\ a_{12}(cos^2\theta-sin^2\theta)+(a_{22}-a_{11}sin\theta\cos\theta& a_{11}sin^2\theta +2a_{12}sin\theta\cos\theta +a_{22}cos^2\theta\end{bmatrix}$

となります。

この非対角項を消去にするには

$a_{12}(cos^2\theta-sin^2\theta)+(a_{22}-a_{11})sin\theta\cos\theta=0$

を解くことになり、両辺をcos²θで割って整理すると

$tan\theta=\frac{-a_{11}-a_{12}\pm\sqrt{(a_{11}-a_{22})^2+4a_{12}^2}}{2a_{12}}$

となり、±を＋で採用すると固有値は大きい順に並びます。

tanθが求まったことから、cosθとsinθが求まります。

$cos\theta=\sqrt{\frac{1}{1+tan^2\theta}}\\ sin\theta=cos\theta\tan\theta$

これで変換行列（回転行列）を求めることが出来ます。

この操作を非対角項全てに対して順番に繰り返し求めることで、最終的には固有値が求まります。また、逐次変換行列同士を掛けて行くことで固有ベクトルが求まります。

使い方

例えば、下記のような対称行列の固有値を計算してみます。

$\begin{bmatrix}4&1&2\\1&3&0\\2&0&5\end{bmatrix}$

3行4列の範囲を指定し、

=eig(行列範囲)

と入力し、CTRL＋SHIFT+ENTERを押します。

CTRL＋SHIFT+ENTERはExcelで配列数式を扱う際の操作になります。

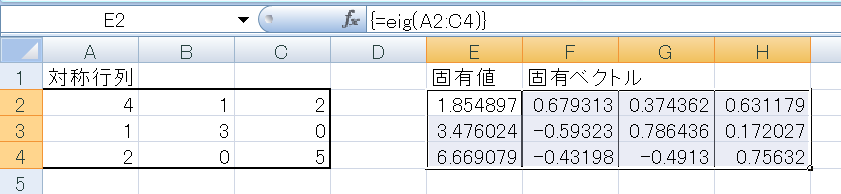
一番左の1列は、固有値

その右側の1列ずつ固有ベクトルとなります。

この例の行列の場合

固有値は

$1.854897309,3.476023603,6.669079088$

固有ベクトルは

$\begin{bmatrix} 0.679313061948559&0.374361954852286&0.63117896877609\\ -0.593233311996296&0.786435698692206&0.172026536791294\\ -0.431981482709593&-0.491296263553547&0.756320024866686 \end{bmatrix}$

となります。

参考資料

CQ出版社、VisualBasicによる固有値計算&振動解析プログラム、黒田英夫著

なお、現在は絶版となっていて、古本はプレミアの値段がついてしまっています。